円形の当たり判定
下はJavaScriptで実装した円形当たり判定のデモ。赤円をドラッグし青円に当てると「HIT!」と表示される。
円形の当たり判定はピタゴラスの定理を使い斜線の距離から割り出す。ピタゴラスの定理とは、直角三角形の斜辺(c)の2乗は他2辺(a, b)をそれぞれ2乗した値の和に等しいという定理。
a² + b² = c²
斜辺以外の2辺の長さが分かれば斜辺の長さも分かる(a + bの値を素因数分解)。下図のように2点間の円形の当たり判定を求める場合、まず直角三角形を作る。
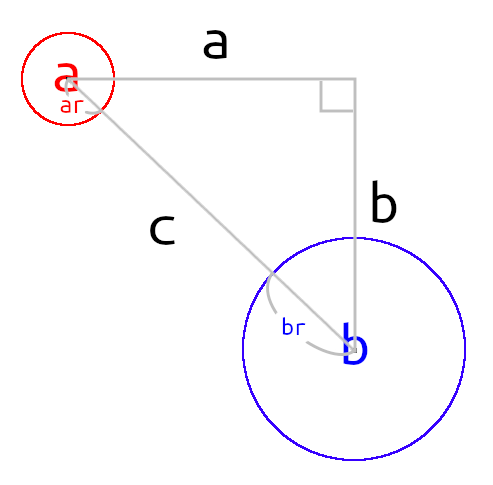
点と点の場合、cが0以下か0を超えるかで判定。円は半径があるため、互いの半径の合計と比較。比較対象が2乗されているので半径も2乗する。当たり判定を求めるだけなら、素因数分解までして正確なcは求めずとも大丈夫。素因数分解して正確な距離を出したい場合はMath.sqrt()を使う。
let dist = Math.sqrt((ax – bx) ** 2 + (ay – by) ** 2);
**はべき乗演算子。左のオペランドを、右のオペランドの累乗にした結果を返す。ここでは2乗している。
まず、円を表示するだけのCircleクラス。
/**
* 真円を描画(circle.js)
*/
export class Circle {
constructor(parent = undefined, x = 0, y = 0, radius = 15) {
if (parent !== undefined) {
this._parent = parent;
}
this._x = x;
this._y = y;
this._radius = radius;
this._color = "#ff0000";
this._init();
}
//////////////////////////////////
// Private and protected
//////////////////////////////////
_init() {
if (this._parent !== undefined) {
this._ctx = this._parent;
}
this.draw();
}
//////////////////////////////////
// Public
//////////////////////////////////
draw() {
this._ctx.save();
this._ctx.fillStyle = this._color;
this._ctx.beginPath();
this._ctx.arc(this._x, this._y, this._radius, 0, (Math.PI * 2), true);
this._ctx.closePath();
this._ctx.fill();
this._ctx.restore();
}
//////////////////////////////////
// Getters/Setters
//////////////////////////////////
get x() {
return this._x;
}
set x(x) {
this._x = x;
}
get y() {
return this._y;
}
set y(y) {
this._y = y;
}
get radius() {
return this._radius;
}
set radius(radius) {
this._radius = radius;
}
set color(color) {
this._color = color;
this.draw();
}
}
次に、当たり判定を行HitTestクラス。
import { Circle } from "./circle.js";
/**
* 当たり判定を行う(hittest.js)
*/
export class Hittest {
constructor() {
this._cvs = document.getElementById('canvas');
this._ctx = this._cvs.getContext('2d');
this._circle1;
this._circle2;
this._isMouseDown = 0;
this._cvs.addEventListener('mousedown', this._onMouseDown.bind(this));
this._onMouseUp = this._onMouseUp.bind(this);
this._onMouseMove = this._onMouseMove.bind(this);
// タイマー関連
this._animID;
this._isAnim = 0;
this._FPS = 60;
this._frame = 0;
this._startTime;
this._nowTime;
this._init();
}
//////////////////////////////////
// Private and protected
//////////////////////////////////
_init() {
this._cvs.style.backgroundColor = "#eeeeee";
this._circle1 = new Circle(this._ctx, 30, 30, 30);
this._circle2 = new Circle(this._ctx, 250, 250, 60);
this._circle2.color = "#0000ff";
this._ctx.font = "30px serif";
this._startTime = performance.now();
this._mainLoop();
}
_mainLoop() {
this._nowTime = performance.now();
let elapsedTime = this._nowTime - this._startTime;
let idealTime = this._frame * (1000 / this._FPS);
if (idealTime < elapsedTime) {
this._ctx.clearRect(0, 0, this._cvs.width, this._cvs.height);
// ①2つの円の当たり判定を行う
let dist = (this._circle1.x - this._circle2.x) ** 2 + (this._circle1.y - this._circle2.y) ** 2;
if (dist <= (this._circle1.radius + this._circle2.radius) ** 2) {
this._ctx.fillText("HIT!", 10, 390);
} else {
this._ctx.fillText("-", 10, 390);
}
this._circle1.draw();
this._circle2.draw();
this._frame++;
if (elapsedTime >= 1000) {
this._startTime = this._nowTime;
this._frame = 0;
}
}
this._animID = requestAnimationFrame(this._mainLoop.bind(this));
}
//////////////////////////////////
// Handlers
//////////////////////////////////
_onMouseDown(e) {
this._isMouseDown = 1 - this._isMouseDown;
this._cvs.addEventListener('mouseup', this._onMouseUp);
this._cvs.addEventListener('mousemove', this._onMouseMove);
}
_onMouseUp(e) {
this._isMouseDown = 1 - this._isMouseDown;
this._cvs.removeEventListener('mouseup', this._onMouseUp);
this._cvs.removeEventListener('mousemove', this._onMouseMove);
}
_onMouseMove(e) {
this._circle1.x = e.clientX;
this._circle1.y = e.clientY;
}
}
①最初にピタゴラスの定理を使い、this._circle1とthis._circle2との距離を測定。当たり判定だけなら2乗したままの値でよい。
次に、距離と2つの円の半径を足して2乗した値を比較。距離の値の方が小さければ当たっている。
requestAnimationFrameを使ったゲームループの実装は、「【JavaScript】requestAnimationFrameでゲームループを作る」を参照。
矩形の当たり判定
下は2匹の猫画像を使った矩形の当たり判定スクリプト
矩形の当たり判定は、2つのオブジェクトのX、Y座標と幅と高さを使い、重なっていれば当たっているとみなす。
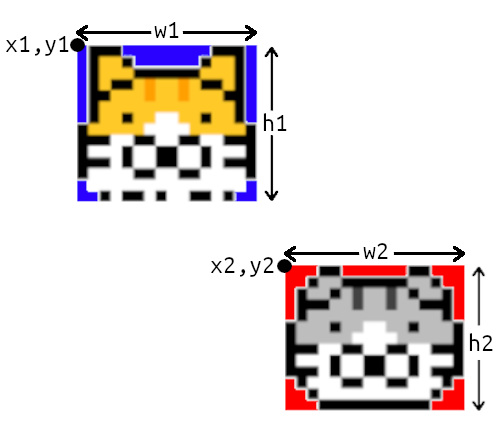
矩形はオブジェクト、例えば画像によっては四隅に何も表示されていない場合もある。そういった事も踏まえ、実際のオブジェクトの大きさより、若干小さくとった方が違和感がない。上のスクリプトは猫画像サイズそのままで当たり判定している。
まず、猫画像を表示するCatクラス。
/**
* 猫画像を表示(cat.js)
*/
export class Cat {
constructor(parent = undefined, x = 0, y = 0, url = "./cat.png") {
if (parent !== undefined) {
this._parent = parent;
}
this._x = x;
this._y = y;
this._rotation = 0;
this._img;
this._imgUrl = url;
this._init();
}
//////////////////////////////////
// Private and protected
//////////////////////////////////
_init() {
if (this._parent !== undefined) {
this._ctx = this._parent;
}
this._img = new Image();
this._img.src = this._imgUrl;
this.draw();
}
//////////////////////////////////
// Public
//////////////////////////////////
draw() {
// 現在の描画状態を保存
this._ctx.save();
// コンテキストの座標を変更し、キャンバス中央に移動
this._ctx.translate(this._x, this._y);
// コンテキストの角度をラジアン値で指定
this._ctx.rotate(this._rotation);
this._ctx.drawImage(this._img, -(this._img.width / 2), -(this._img.height / 2));
// save()で保存した描画状態を復元
this._ctx.restore();
}
//////////////////////////////////
// Getters/Setters
//////////////////////////////////
get x() {
return this._x;
}
set x(x) {
this._x = x;
}
get y() {
return this._y;
}
set y(y) {
this._y = y;
}
get width() {
return this._img.width;
}
get height() {
return this._img.height;
}
get rotation() {
return this._rotation;
}
set rotation(rotation) {
this._rotation = rotation;
}
}
次に、当たり判定を行うHitTest2クラス。
import { Cat } from "./cat.js";
/**
* 矩形の当たり判定を行う(hittest2.js)
*/
export class Hittest2 {
constructor() {
this._cvs = document.getElementById('canvas');
this._ctx = this._cvs.getContext('2d');
this._cat;
this._cat2;
this._isMouseDown = 0;
this._cvs.addEventListener('mousedown', this._onMouseDown.bind(this));
this._onMouseUp = this._onMouseUp.bind(this);
this._onMouseMove = this._onMouseMove.bind(this);
// タイマー関連
this._animID;
this._isAnim = 0;
this._FPS = 60;
this._frame = 0;
this._startTime;
this._nowTime;
this._init();
}
//////////////////////////////////
// Private and protected
//////////////////////////////////
_init() {
this._cvs.style.backgroundColor = "#eeeeee";
this._cat = new Cat(this._ctx, 50, 50);
this._cat2 = new Cat(this._ctx, 250, 250, "./cat2.png");
this._ctx.font = "30px serif";
this._startTime = performance.now();
this._mainLoop();
}
_mainLoop() {
this._nowTime = performance.now();
let elapsedTime = this._nowTime - this._startTime;
let idealTime = this._frame * (1000 / this._FPS);
if (idealTime < elapsedTime) {
this._ctx.clearRect(0, 0, this._cvs.width, this._cvs.height);
// ①2つの矩形の当たり判定を行う
if (
this._cat.x < this._cat2.x + this._cat2.width &&
this._cat.x + this._cat.width > this._cat2.x &&
this._cat.y < this._cat2.y + this._cat2.height &&
this._cat.y + this._cat.height > this._cat2.y)
{
this._ctx.fillText("HIT!", 10, 390);
} else {
this._ctx.fillText("-", 10, 390);
}
this._cat.draw();
this._cat2.draw();
this._frame++;
if (elapsedTime >= 1000) {
this._startTime = this._nowTime;
this._frame = 0;
}
}
this._animID = requestAnimationFrame(this._mainLoop.bind(this));
}
//////////////////////////////////
// Handlers
//////////////////////////////////
_onMouseDown(e) {
this._isMouseDown = 1 - this._isMouseDown;
this._cvs.addEventListener('mouseup', this._onMouseUp);
this._cvs.addEventListener('mousemove', this._onMouseMove);
}
_onMouseUp(e) {
this._isMouseDown = 1 - this._isMouseDown;
this._cvs.removeEventListener('mouseup', this._onMouseUp);
this._cvs.removeEventListener('mousemove', this._onMouseMove);
}
_onMouseMove(e) {
this._cat.x = e.clientX;
this._cat.y = e.clientY;
}
}
参考図書

コメント