キャンバス上に矢印を描画して、常にマウスポインタの方に向けさせる。つまり、矢印はその場で回転する。
ArrowクラスとRotateクラス
まず、矢印を描画するArrowクラスを作成。
/**
* arrow.js
* 矢印の作成と描画
*/
export class Arrow {
constructor(parent = undefined, x = 0, y = 0) {
if (parent !== undefined) {
this._parent = parent;
}
this._x = x;
this._y = y;
this._color = "#ffff00";
this._rotation = 0;
this._init();
}
//////////////////////////////////
// Private and protected
//////////////////////////////////
_init() {
if (this._parent !== undefined) {
this._ctx = this._parent;
}
this.draw();
}
//////////////////////////////////
// Public
//////////////////////////////////
draw() {
// 現在の描画状態を保存
this._ctx.save();
// コンテキストの座標を変更し、キャンバス中央に移動
this._ctx.translate(this._x, this._y);
// ②コンテキストの角度をラジアン値で指定
this._ctx.rotate(this._rotation);
this._ctx.fillStyle = this._color;
this._ctx.beginPath();
this._ctx.moveTo(-50, -25);
this._ctx.lineTo(0, -25);
this._ctx.lineTo(0, -50);
this._ctx.lineTo(50, 0);
this._ctx.lineTo(0, 50);
this._ctx.lineTo(0, 25);
this._ctx.lineTo(-50, 25);
this._ctx.lineTo(-50, -25);
this._ctx.closePath();
this._ctx.fill();
this._ctx.stroke();
// save()で保存した描画状態を復元
// 変形情報(translate、rotate)を変更前に戻している
this._ctx.restore();
}
//////////////////////////////////
// Getters/Setters
//////////////////////////////////
get x() {
return this._x;
}
set x(x) {
this._x = x;
}
get y() {
return this._y;
}
set y(y) {
this._y = y;
}
get rotation() {
return this._rotation;
}
set rotation(rotation) {
this._rotation = rotation;
}
}
rotate.jsは、キャンバス上をマウスポインタが動く度にmousemoveイベントを実行。ハンドラ内で回転させる角度の計算し、その結果を元に矢印の再描画を行う。
import { Arrow } from "./arrow.js";
/**
* rotate.js
* 回転処理を担当
*/
class Rotate {
constructor() {
this._cvs = document.getElementById('canvas');
this._ctx = this._cvs.getContext('2d');
this._arrow;
this._cvs.addEventListener('mousemove', this._onMouseMove.bind(this));
this._init();
}
//////////////////////////////////
// Private and protected
//////////////////////////////////
_init() {
this._cvs.style.backgroundColor = "#ccc";
this._arrow = new Arrow(this._ctx, this._cvs.width / 2, this._cvs.height / 2);
}
//////////////////////////////////
// Handlers
//////////////////////////////////
_onMouseMove(e) {
this._ctx.clearRect(0, 0, this._cvs.width, this._cvs.height);
let dx = e.clientX - this._arrow.x;
let dy = e.clientY - this._arrow.y;
// ①角度(ラジアン単位)を求める
this._arrow.rotation = Math.atan2(dy, dx);
this._arrow.draw();
}
}
let run = new Rotate();
回転処理は三角関数を使い実装している。そのため、まず三角関数の簡単な説明から行う。
三角関数について
まず、直角三角形のそれぞれの箇所の名称。直角三角形では直角(90度の部分)の反対側にある辺を斜辺と呼ぶ。3つの辺で最も長い辺。
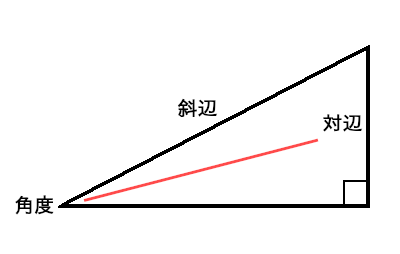
ある角度の反対側にある辺を対辺と呼ぶ。どの角度を選んだかで対辺は変化する。上図の場合、左下の角度から見れば対辺は右の縦の辺。
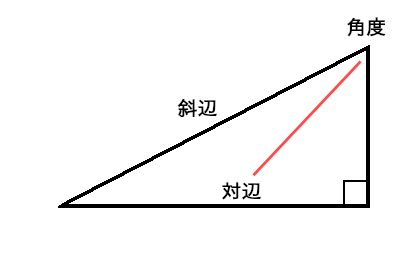
右上の角度から見れば下の横の辺。
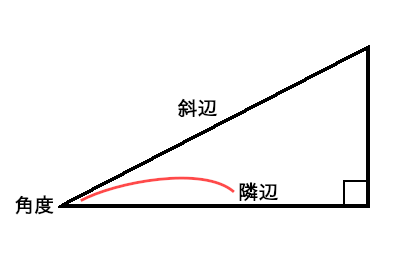
ある角度に接している斜辺以外の辺を隣辺と呼ぶ。どの角度を選んだかで隣辺は変化する。上図の場合、左下の角度から見れば隣辺は下の横の辺。
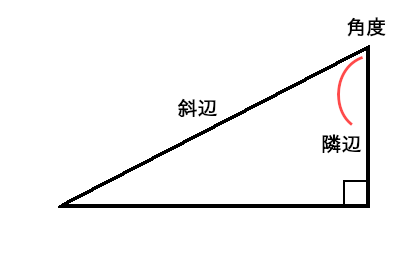
右上の角度から見れば右の縦の辺。
角度とラジアン
ラジアン(弧度法)についてここでは詳解しないが、プログラミングでは度よりラジアンが使われる。度をラジアンに変換、またラジアンを度に変換する式は以下。Math.PIは円周率(π)のこと。
- ラジアン = 度 * Math.PI / 180;
- 度 = ラジアン * 180 / Math.PI;
JavaScriptの座標系と角度の測定方法
説明を進める前に、以下の知識を覚えておく必要がある。
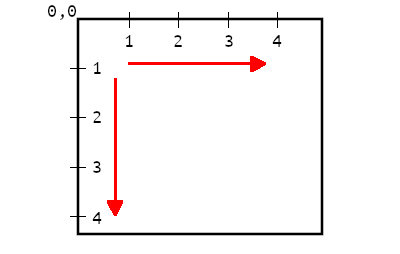
JavaScriptの座標系は左上隅を(0,0)とし、X値は右に行くほど増え(正)、左に行くほど減り(負)、Y値は下へ行くほど増え(正)、上に行くほど減る(負)。
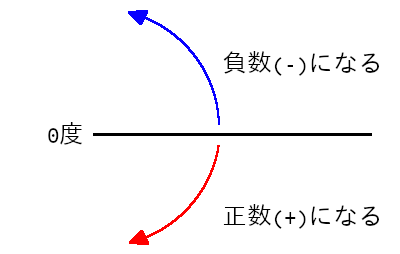
角度の測定は0度をX軸方向に伸びる直線として表され、 そこから正の値は時計回り、負の値は反時計回りに計測される。
サイン(正弦)とアークサイン
サインは、ある角度の対辺の斜辺に対する比率を表す。対辺 ÷ 斜辺。Math.sin(角度)で取得できる。角度はラジアン単位で渡す。
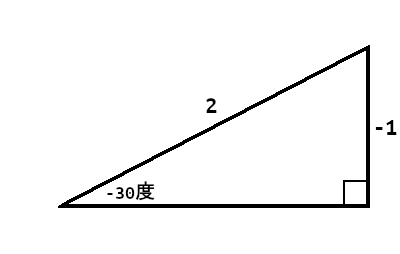
JavaScriptではY軸は上に行くと負の値になり、角度は反時計回りでは負の値になる。そのため、上図では角度と対辺の値は負の値になっている。
仮に上図の三角形の左下の角度が30度なら、Math.sin(-30 * Math.PI / 180)で約-0.5が返ってくる。これは上図の三角形の対辺と斜辺の比率が1対2、つまり-1/2で少数に直すと-0.5だからだ。2進数で計算するコンピュータは0.4999…と表示されるが、誤差は非常に小さく無視して大丈夫。
アークサインはサインの逆で、比率(対辺と斜辺の)を渡すと角度をラジアン単位で返す。Math.asin(比率)。
コサイン(余弦)とアークコサイン
コサインは、ある角度の隣辺の斜辺に対する比率を表す。隣辺 ÷ 斜辺。Math.cos(角度)で取得できる。角度はラジアン単位で渡す。
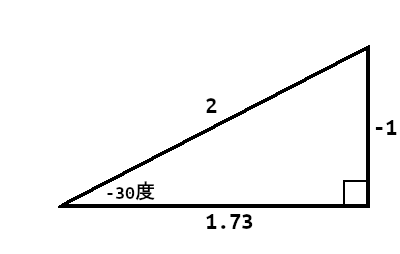
上画像の場合、Math.cos(-30 * Math.PI / 180)で、約0.866が返ってくる。隣辺は1.73で1.73/2だからだ。
アークコサインはコサインの逆で、比率(隣辺と斜辺の)を渡すと角度をラジアン単位で返す。Math.acos(比率)。
タンジェント(正接)とアークタンジェント
タンジェントは、ある角度の対辺の隣辺に対する比率を表す。対辺 ÷ 隣辺。Math.tan(角度)で取得できる。角度はラジアン単位で渡す。

上画像の場合、Math.tan(-30 * Math.PI / 180)で、約-0.577が返ってくる。
アークタンジェントはタンジェントの逆で、比率(対辺と隣辺の)を渡すと角度をラジアン単位で返す。Math.atan(比率)。しかし、Math.atan()には問題がある。
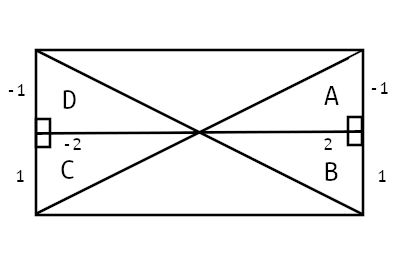
上図では4つの三角形があり、中央の角度は全て約26.57度。AとBのX値は正の値、CとDは負の値を持つ。さらに AとDのY値は負の値、BとCは正の値を持つ。各それぞれのタンジェント(対辺の隣辺に対する比率)は、
- A:-0.5
- B:0.5
- C:-0.5
- D:0.5
となる。Math.atan()で角度を求めようと、0.5や-0.5を渡した場合、BとD、AとC、どちらの三角形のことなのか判別できない。その対策としてJavaScriptではもう一つのMath.atan2()が提供されている。
Math.atan()は比率を渡すと角度をラジアン単位で返したが、Math.atan2()は対辺の長さと隣辺の長さの2つの引数を元に角度をラジアン単位で返す。
Math.atan2(対辺の長さ, 隣辺の長さ);
三角形BとDはMath.atan() * 180 / Math.PIでは共に26.56度だが、Math.atan2() * 180 / Math.PIでは以下のように区別がつく。
- B:26.56度
- D:-153.43度
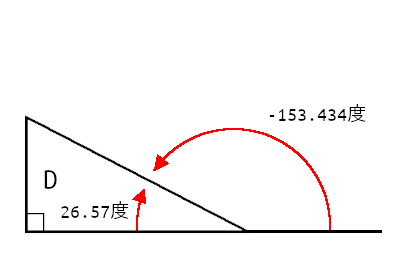
三角形Dが-153.43度なのは、「JavaScriptの座標系と角度の測定方法」での説明を参照。
Math.atan2()で矢印を回転
rotate.jsのコード①が回転処理を行っている部分。Math.atan2()にマウスカーソスのX座標、Y座標を渡して、角度のラジアン単位を受け取る。角度をthis._arrowオブジェクトのrotationに渡し、draw()を呼ぶ。
draw()内では変更された角度を元に(arrow.jsのコード②)、Canvas上の矢印が再描画される。これをマウスカーソルが動く度に繰り返している。
index.htmlが以下。
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<meta http-equiv="Content-Type" content="text/html; charset=UTF-8">
<title>オブジェクトの回転</title>
</head>
<body>
<canvas id="canvas" width="400" height="400"></canvas>
</body>
<script type="module" src="./rotate.js"></script>
</html>参考図書



コメント